Гэтая матэматычная задача пра дзень нараджэння зломіць вам мозг
Знакамітая «Праблема дня нараджэння» не перастае здзіўляць людзей. Праверце, ці зможаце вы хаця б наблізіцца да адказу.
Задача
Кастусь і Алеся прымаюць запрашэнне на хатнюю вечарыну. Кастусь бачыць, што на вечарыне будзе 30 чалавек, і кажа Алесі: «Б'юся аб заклад на 100 даляраў, што як мінімум два чалавекі будуць святкаваць там аднолькавы дзень нараджэння!»
Ці варта Алесі прыняць гэтую стаўку? (Дапусцім, што дні нараджэння размеркаваныя пароўну на працягу года з 365 дзён.)
Падказка
Вам можа спатрэбіцца формула і Excel-табліца.
Рашэнне ніжэй пад фота.

Рашэнне
Самы просты спосаб рашыць гэту задачу — пайсці ад адваротнага: якая верагоднасць таго, што ў групе пэўнага памеру ніхто не будзе мець аднолькавых дзён нараджэння?
Давайце разгледзім групу з пяці чалавек. Першы чалавек будзе мець нейкі выпадковы дзень нараджэння паміж 1 студзеня і 31 снежня. У такім выпадку ў другога чалавека будзе імавернасць (364/365) таго, што дзень нараджэння не будзе супадаць з днём нараджэння першага чалавека. Такім чынам, у трэцяга чалавека ёсць 363 «свабодныя» даты на выбар, значыць, імавернасць таго, што дзень нараджэння не будзе супадаць з днём нараджэння першага або другога чалавека, складае 363/365. Чацвёрты чалавек будзе мець шанец 362/365 не дзяліць свой дзень з іншым і гэтак далей.
Каб потым атрымаць імавернасць таго, што ні ў аднаго з пяці чалавек не будзе агульнага дня нараджэння, нам трэба перамножыць гэтыя імавернасці разам:
P = (364/365)*(363/365)*(362/365)*(361/365) = 0,97
Іншымі словамі, у кампаніі з пяці чалавек чалавек не будзе мець агульнай даты нараджэння з імавернасцю 97 адсоткаў. Гэта здаецца даволі інтуітыўна зразумелым і азначае, што ёсць толькі 3% імавернасці, што як мінімум два чалавекі будуць мець агульную дату.
Што можа быць менш інтуітыўна зразумелым, дык гэта тое, як хутка расце гэтая лічба. У табліцы ніжэй выкарыстоўваецца той жа разлік, каб паказаць імавернасць таго, што як мінімум два чалавекі будуць мець адзін і той жа дзень нараджэння ў залежнасці ад колькасці чалавек у групе:
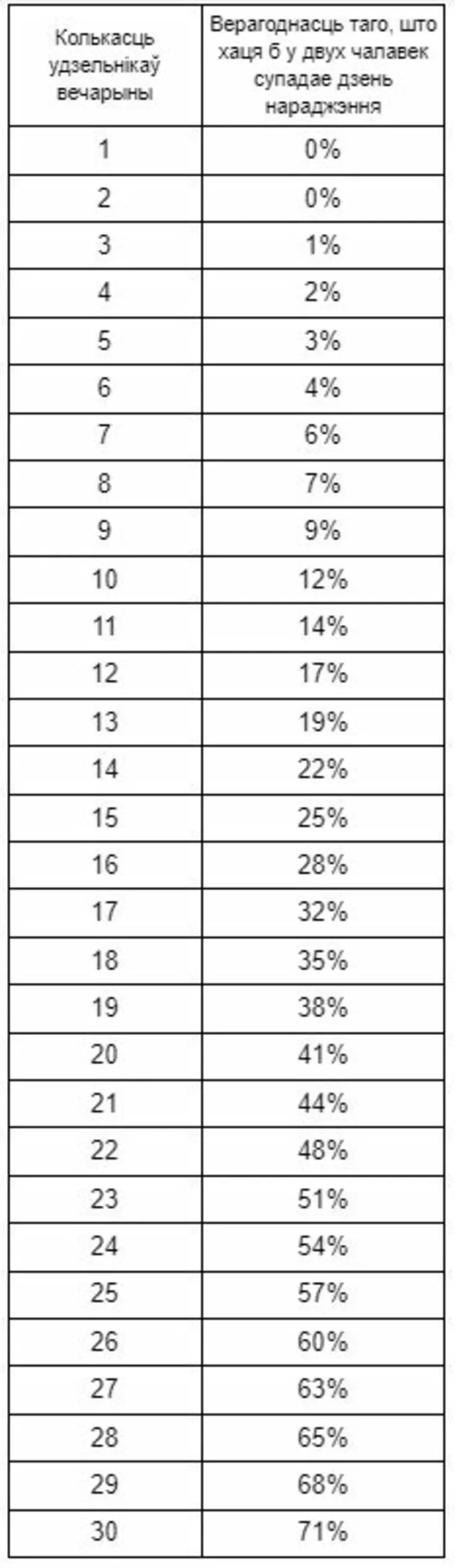
У групе з 30 чалавек існуе 71% імавернасці, што ў двух чалавек будзе супадаць дзень нараджэння. Таму Алесі лепей не прымаць гэтую стаўку!
Вы можаце праверыць гэта на бліжэйшай сустрэчы выпускнікоў, вяселлі ці юбілеі.







































Каментары